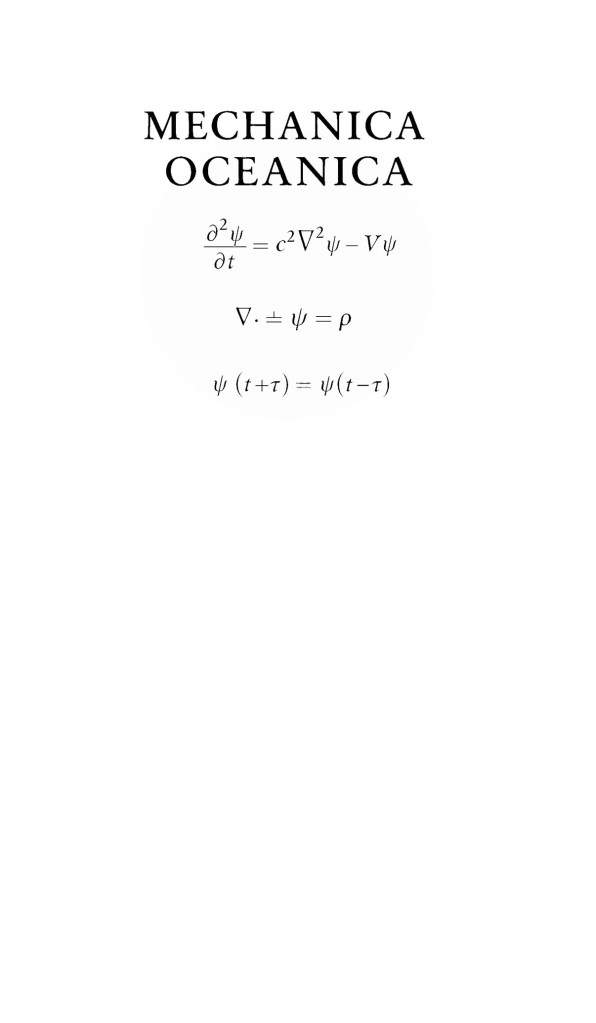
Introduction: Space as a Tensioned Medium
Imagine the fabric of space as an enormous, invisible ocean – not empty void, but a medium under tension. This is the core principle of the “oceanic” electromagnetic model. In this view, what we call vacuum is actually a taut, all-pervading field capable of oscillation, much like a stretched membrane or a vast taut fluid. Waves of electromagnetism (light, radio waves, etc.) are then interpreted as vibrations of this underlying medium, instead of abstract fields existing in empty space. Historically, scientists like Michael Faraday pictured electric and magnetic lines of force as physicallines under tension in an ether . James Clerk Maxwell initially went down a similar path, envisioning a mechanical ether model for electromagnetism – he spoke of “molecular vortices” in a fluid-like medium to model magnetic lines of force . In essence, the oceanic model revives and refines this intuition: it treats space as a physical continuum that can carry waves. The term “tensioned medium” means that this continuum resists compression or stretching, storing energy when disturbed (much like a stretched guitar string stores energy when plucked). If we pluck or disturb the fabric of space, waves propagate through it. The goal of this exposition is to develop a rigorous wave equation for this medium from first principles, define precise analogues of electric and magnetic fields arising from the single underlying field \Psi, and show how Maxwell’s equations emerge naturally from the dynamics of \Psi. We will compare this model to Newtonian mechanics, classical wave theory, and Maxwell’s standard electromagnetism – highlighting differences and why they matter. Finally, we will discuss why this mechanical picture of electromagnetism was historically overlooked and how it reframes our understanding, along with ways one might experimentally detect if space indeed behaves like a “tensioned ocean.”
From Newton to Waves: Deriving the Master Equation
To formulate the oceanic model, we begin with a simple physical analogy: think of a taut rope or a stretched rubber membrane. If you displace a small segment, the tension in the material pulls it back toward equilibrium, and the disturbance travels outward as a wave. In three-dimensional space, we imagine the underlying field \Psi(\mathbf{r}, t) as describing the displacement of each point of the space-medium. For clarity, \Psi can be treated as a vector field \Psi = ( \Psi_x, \Psi_y, \Psi_z ) representing a tiny “shift” or “offset” of the medium at point \mathbf{r}. When undisturbed, \Psi = 0 everywhere (the medium is at rest). When \Psi is nonzero in some region, the medium there is locally displaced or strained.
Assumptions of the medium: We assume the medium has two essential properties, analogous to any elastic material: an inertial density (mass per volume, denoted \rho) and an effective tension (or elastic restoring force, denoted T). In loose terms, \rho tells us how hard it is to accelerate a portion of the medium (inertia), and T tells us how strongly the medium resists deformation (stiffness or tension). These properties will determine the speed at which waves propagate through the medium. Just as waves on a string have speed v = \sqrt{T/\mu} (tension over linear mass density), and sound waves have speed \sqrt{K/\rho} (bulk modulus over density), electromagnetic waves will emerge with speed c = \sqrt{T/\rho}. We will later identify this c with the observed speed of light.
Newton’s second law applied to the medium: Consider a small element of the space-medium. When \Psi has curvature or distortion, neighboring regions of the medium pull on this element. The net force on a small volume can be expressed in terms of spatial derivatives of \Psi. A simple, linearly elastic model yields a force density proportional to the Laplacian of \Psi. Intuitively, \nabla^2 \Psi measures how \Psi at a point differs from the average of \Psi in a small surrounding region – it’s nonzero when \Psi is “curved” or has tension pulling it back toward equilibrium. If T is the tension coefficient, the force (per unit volume) on the medium is approximately -\,T\,\nabla^2 \Psi. By Newton’s law (force = mass × acceleration), we equate this to the inertial force density \rho \,\partial^2 \Psi/\partial t^2 (mass density times acceleration of the medium element). This yields the wave equation for the field \Psi(\mathbf{r},t):
\rho\,\frac{\partial^2 \Psi}{\partial t^2} \;=\; T\,\nabla^2 \Psi \,. \tag{1}
Rewriting, we get a more familiar form:
\frac{\partial^2 \Psi}{\partial t^2} \;=\; \frac{T}{\rho}\,\nabla^2 \Psi \;=\; c^2\, \nabla^2 \Psi \,, \tag{2}
where we identify c = \sqrt{T/\rho} as the characteristic wave speed in the medium. Equation (2) is a classical linear wave equation. It implies that small disturbances in \Psi propagate as waves with speed c. Notably, if we plug in the values of T and \rho required to make c equal to the observed speed of light (~3\times10^8 m/s), we find the medium must have an enormous tension or extremely low density (or both), which is why we don’t notice any drag or resistance from this medium in everyday life – it is exceptionally “light” yet extraordinarily stiff. (In fact, 19th-century physicists realized that if an ether existed, it had to have very unusual properties: extremely high rigidity to support light’s high speed, yet no viscosity or drag on moving objects .)
Meaning of the wave equation: Every component of \Psi satisfies \partial_{tt} \Psi_i = c^2\, \nabla^2 \Psi_i. Physically, this means if part of the medium is displaced (say, pushed upward in the x-direction), a restoring force pulls it back, and inertia causes overshoot – resulting in oscillatory motion that propagates outward. It’s exactly analogous to waves on a taut drumhead or waves in a Jell-O dessert: the medium’s tension and inertia allow transverse ripples to travel. In our case, “transverse” means the displacement \Psi can be perpendicular to the direction of wave travel – a hallmark of electromagnetic waves which are transverse oscillations. Importantly, the form of Eq. (2) does not pick out any preferred direction or frame of motion; it has the same form under rotations and (as we will discuss later) it can be consistent with the principle of relativity if handled carefully. For now, Eq. (2) is the master equation of the medium, from which we will derive the analogues of electric and magnetic fields and ultimately the full set of Maxwell-like equations.
Fields from the Field: Defining Electric and Magnetic Components
How do the electric (\mathbf{E}) and magnetic (\mathbf{B}) fields arise from the single underlying field \Psi? In the oceanic model, \Psi(\mathbf{r},t) is more fundamental – \mathbf{E} and \mathbf{B} are secondary fields describing different aspects of \Psi’s disturbance. We choose definitions that will make a seamless connection to Maxwell’s equations:
• Magnetic Field (\mathbf{B}) – We define \displaystyle \mathbf{B}(\mathbf{r},t) \equiv \nabla \times \Psi(\mathbf{r},t). In words, \mathbf{B} is the local “curl” or rotation of the displacement field \Psi. This choice is motivated by Maxwell’s insight that magnetic field lines resemble vortex lines in a fluid . If \Psi circulates (whirls) around some axis, it produces a magnetic field along that axis (much as looping currents produce magnetic lines). By defining \mathbf{B} = \nabla \times \Psi, we automatically satisfy one of Maxwell’s equations: the divergence of a curl is always zero, so \nabla \cdot \mathbf{B} = 0. This captures Gauss’s law for magnetism (no magnetic monopoles, magnetic field lines have no beginning or end) as an identity rather than an empirical law – it holds for any field defined as a curl.
• Electric Field (\mathbf{E}) – We define \displaystyle \mathbf{E}(\mathbf{r},t) \equiv -\,\frac{\partial \Psi(\mathbf{r},t)}{\partial t}. In words, \mathbf{E} is (minus) the time-rate-of-change of the displacement field \Psi. This definition is inspired by the physical idea that a changing displacement (motion or acceleration of the medium) should correspond to an electric effect. Remember, in electromagnetism an electric field is what exerts force on charges. Here, if \Psi starts moving, it implies a force is acting (Newton’s second law for the medium element). We insert a minus sign so that -\partial \Psi/\partial t will end up playing the role of force density on external charges (the sign convention will become clear in the Faraday’s law derivation below). With this definition, a static (unchanging) displacement field would produce no electric field, which aligns with the idea that a static distortion in the medium might correspond to a magnetic-only configuration (like a steady magnetostatic vortex that has no electric field unless it changes).
These definitions of \mathbf{E} and \mathbf{B} are straightforward and natural for a medium in which \Psi is the fundamental dynamical variable. They capture the intuitive picture: \mathbf{B} is associated with how \Psi twists around (a swirling of the medium corresponds to magnetic field lines), and \mathbf{E} is associated with how \Psi evolves in time (a rapidly changing or accelerating portion of the medium corresponds to an electric field). We will now show that these definitions, plugged into the master wave equation (2), yield the full set of Maxwell-like equations. Each “Maxwell equation” emerges as either an identity or a consequence of the wave equation.
From the Master Equation to Maxwell’s Equations
Starting from the master wave equation (Eq. 2) and our field definitions, we can derive analogues of Maxwell’s four equations step by step:
• Gauss’s Law for Magnetism (\nabla \cdot \mathbf{B} = 0): As noted above, \mathbf{B} = \nabla \times \Psi implies \nabla \cdot \mathbf{B} = \nabla \cdot (\nabla \times \Psi) = 0 identically. This matches Maxwell’s law that there are no magnetic monopoles – magnetic field lines form closed loops. In the medium picture, this is geometrically obvious: \mathbf{B} arises from a curling of \Psi, and one cannot have “sources” or “sinks” of a pure curl field (just as a whirlpool has no beginning or end point in the water). Every magnetic field line in this model is a loop of circulating \Psi in the medium .
• Faraday’s Law of Induction (\nabla \times \mathbf{E} = -\,\partial \mathbf{B}/\partial t): We compute the curl of \mathbf{E} using our definition \mathbf{E} = -\,\partial_t \Psi. Since curl and time-derivative can be interchanged (assuming nice continuous fields), \nabla \times \mathbf{E} = -\,\nabla \times (\partial_t \Psi) = -\,\partial_t (\nabla \times \Psi). But \nabla \times \Psi = \mathbf{B}. Thus, \nabla \times \mathbf{E} = -\,\partial \mathbf{B}/\partial t. This is exactly Faraday’s law, which states a time-changing magnetic field induces an electric field (with the minus sign indicating Lenz’s law direction). Here it isn’t an experimentally deduced law but a mathematical consequence of our definitions: it basically says “the curl of the time-change of \Psi equals the time-change of the curl of \Psi” – a symmetry of mixed derivatives. Physically, it means if the medium’s vortex (magnetic field) intensity changes with time, it is accompanied by a curling electric field. In the medium picture, a decreasing vortex (magnetic) implies the medium’s motion has a curl – the surrounding medium “circulates” in such a way as to create an electric field. This matches exactly what Faraday’s induction describes.
• Ampère–Maxwell Law (\nabla \times \mathbf{B} = \frac{1}{c^2}\,\partial \mathbf{E}/\partial t, in free space): This is the more involved part – it comes from the dynamical equation (the wave equation). Take the curl of \mathbf{B}: \nabla \times \mathbf{B} = \nabla \times (\nabla \times \Psi). There is a vector calculus identity \nabla \times (\nabla \times \Psi) = \nabla(\nabla \cdot \Psi) – \nabla^2 \Psi. Thus,
\nabla \times \mathbf{B} = \nabla(\nabla \cdot \Psi)\;-\;\nabla^2 \Psi\,.
Now, if the medium is incompressible or the disturbances are purely transverse, we have \nabla \cdot \Psi = 0 (this was actually a condition Maxwell assumed in his mechanical model to avoid longitudinal waves – we will discuss this assumption shortly). Under this condition, the first term vanishes, giving \nabla \times \mathbf{B} = -\,\nabla^2 \Psi. But from the wave equation (2), \nabla^2 \Psi = \frac{1}{c^2}\,\partial^2 \Psi/\partial t^2. Therefore,
\nabla \times \mathbf{B} = -\,\frac{1}{c^2}\,\frac{\partial^2 \Psi}{\partial t^2}\,.
Now notice that \partial \mathbf{E}/\partial t = \partial(-\partial_t \Psi)/\partial t = -\,\partial^2 \Psi/\partial t^2. So substitute this in:
\nabla \times \mathbf{B} = \frac{1}{c^2}\,\frac{\partial \mathbf{E}}{\partial t}\,.
And there we have Ampère’s law (for vacuum, with no current term). This equation says a changing electric field produces a magnetic circulation. In our model, it came from the medium’s equation of motion – essentially Newton’s law for the medium. We did use \nabla \cdot \Psi = 0 in the derivation. What does that assumption mean physically? It means we are considering disturbances where the medium’s displacement has no net divergence – in other words, we’re not compressing regions of the medium like sound waves, but only shearing or twisting it (transverse waves). This aligns with the observed nature of light: electromagnetic waves in free space are transverse. We will discuss later the possibility of \nabla \cdot \Psi \neq 0, but for now, this condition is taken as part of modeling electromagnetism specifically. Under it, Ampère’s circuital law with Maxwell’s displacement current term emerges cleanly. The term \frac{1}{c^2}\partial \mathbf{E}/\partial t is the “displacement current” in Maxwell’s terms – here it arose from the medium’s inertia (the fact that a time-changing electric field corresponds to accelerating medium elements, which by Newton’s law generate a curl in \Psi, i.e. a magnetic response).
• Gauss’s Law for Electricity (\nabla \cdot \mathbf{E} = 0 in free space): Finally, consider the divergence of \mathbf{E}. Using \mathbf{E} = -\partial_t \Psi:
\nabla \cdot \mathbf{E} = -\,\nabla \cdot (\partial_t \Psi) = -\,\partial_t (\nabla \cdot \Psi)\,.
If we again assume \nabla \cdot \Psi = 0 as an initial (and continuing) condition for the kind of waves we’re interested in, then \nabla \cdot \mathbf{E} = 0 at all times. This is the source-free Gauss’s law: no net electric charge density in the regions of vacuum we’re considering, so the electric field lines have no divergence (any field lines that start somewhere must end somewhere, typically on charges – with no charges present, if a field line enters a volume it must also exit). In a source-free scenario, \nabla \cdot \mathbf{E}=0 is automatically satisfied in this model by virtue of the divergence-free motion of the medium. If we were to introduce charges into the picture, \nabla \cdot \Psi would no longer be zero at those points – a charge could be represented by a kind of defect or source of \Psi in the medium (imagine a point where the medium has a sink or source, creating divergence). That would alter Gauss’s law to \nabla \cdot \mathbf{E} \neq 0 proportional to the charge. But handling charges and source terms is beyond our current scope – we’re focusing on free electromagnetic waves and fields. So for now, Gauss’s law for electricity holds (with zero on the right-hand side), consistent with our vacuum wave model.
In summary, by starting from the single field \Psi and its wave equation, and defining \mathbf{E} and \mathbf{B} in a natural way, we have obtained all four of Maxwell’s equations (in their free-space form) as logical consequences:
• Gauss (magnetic): \nabla \cdot \mathbf{B} = 0 (true for any \mathbf{B}=\nabla\times\Psi)
• Faraday’s law: \nabla \times \mathbf{E} = -\,\partial \mathbf{B}/\partial t (from mixed space-time derivative symmetry)
• Ampère’s law: \nabla \times \mathbf{B} = \frac{1}{c^2}\,\partial \mathbf{E}/\partial t (from the wave equation for \Psi, assuming divergence-free medium)
• Gauss (electric): \nabla \cdot \mathbf{E} = 0 (no charges in medium, ensured by initial \nabla\cdot\Psi=0).
It’s remarkable that what Maxwell formulated as four separate empirical laws here emerge from a single postulate: that space is a dynamical medium governed by a wave equation. In this sense, the oceanic model unifies the electric and magnetic fields – they are just different facets of one deeper field \Psi. In technical terms, \Psi plays a role analogous to the electromagnetic four-potential ( \Phi, \mathbf{A} ) in standard theory, but here it has a clear physical interpretation as the medium’s displacement field. And unlike in Maxwell’s 19th-century conception where the ether was somewhat mysterious, we have explicitly laid out its equation of motion. This single-field framework gives a satisfying explanation for why the electric and magnetic fields are always found together, linked by Maxwell’s equations – in the model they are literally born from the same oscillations of \Psi.
Before moving on, let’s explicitly note one thing: we assumed \nabla \cdot \Psi = 0 to derive the tidy set of equations above. This assumption basically “throws out” any longitudinal wave solutions of Eq. (2), focusing only on transverse waves. In a normal elastic medium, longitudinal (compressional) waves are also possible (think of sound waves in a solid). If the space-medium allowed longitudinal disturbances, they would be a different kind of field (some researchers might associate them with other physical phenomena or perhaps they’re suppressed for electromagnetic interactions). The fact that we don’t detect any propagating longitudinal electromagnetic field suggests that either the medium is effectively incompressible, or any compressive modes do not couple to charges in a straightforward way. For now, the model idealizes space as an incompressible, purely tensioned medium for electromagnetic disturbances – hence only transverse waves (light) propagate. We will revisit this point later when discussing experimental tests.
Comparisons with Established Theories
It’s helpful to pause and compare the oceanic electromagnetic model with three pillars of physics that it draws upon: Newtonian mechanics, classical wave theory, and Maxwell’s classical electromagnetism. By highlighting similarities and differences, we can appreciate what’s truly new here and what is merely a translation of known physics into a different language.
Newtonian Mechanics vs. Field Mechanics
At its heart, the derivation we performed is entirely Newtonian in spirit – we applied F = ma to a tiny chunk of a medium. This is a key difference from how Maxwell’s equations are usually introduced. In Maxwell’s standard theory, the fields \mathbf{E} and \mathbf{B} are fundamental and obey rules that were inferred from experiments (Coulomb’s law, Faraday’s induction, etc.), with no underlying mechanism specified. Here, we suppose a mechanism: a physical medium whose elements obey Newton’s second law. All the complexity of electromagnetic phenomena is, in principle, reducible to the dynamics of this medium. In a Newtonian analogy, you can think of each point in space as a tiny mass on springs connected to its neighbors – if you push one, they all start moving according to Newton’s laws, and a disturbance travels. This model thus reduces electromagnetism to a mechanical system, which is conceptually appealing to those who like tangible explanations.
What’s different from everyday Newtonian mechanics is that we are dealing with a continuum field, not point particles. Newton’s laws are applied locally (via density and tension) rather than to discrete masses. But that’s standard in continuum mechanics (fluids, solids). The form of Eq. (1) or (2) is exactly what you get for small oscillations of a homogeneous, isotropic medium – nothing exotic in a mechanical sense. Another difference is the scale and properties: this medium must be extraordinary (as mentioned, possibly extremely stiff yet invisible to direct detection). Newtonian intuition might expect that if space is a substance, moving through it would cause drag or that it would have some “wind” effect. But the model’s consistency with relativity (next section) ensures that in uniform motion one cannot detect any effect of a “medium wind” – a non-intuitive but necessary feature if Newtonian mechanics in the medium is to coexist with the relativity of inertial frames. In summary, the oceanic model is deeply grounded in Newtonian mechanics applied to a field. It doesn’t overthrow F=ma; rather, it extends it to every point of space. This is a reframing of electromagnetism in terms of forces and inertia in a medium, as opposed to the more abstract classical field concept where fields carry momentum and energy without explicit mass or force carriers. (Interestingly, Maxwell himself stated that explaining electromagnetic forces by stress in a medium was simply following Faraday’s conception, with field lines acting like stretched elastic threads .)
Classical Wave Theory Analogies
The model is also strongly rooted in classical wave theory. Equation (2) is recognizable as the classic wave equation, which appears in countless physical contexts. For example, a vibrating string, sound waves in air, or ripples on a water surface all satisfy analogous equations. By casting Maxwell’s equations into the form of a wave equation for \Psi, we see electromagnetic waves as just another case of the universal phenomenon of waves. This is satisfying because it ties light to a familiar concept: waves require a medium to propagate in classical physics, so here we supply that medium. In the 19th century, this was exactly the reasoning – since water waves need water and sound needs air, light must need an ether. The oceanic model wholeheartedly embraces that analogy, rather than sidestepping it as modern physics did.
However, there are important differences from typical wave media:
• Transverse vs Longitudinal: Most everyday waves (sound, for instance) are longitudinal pressure waves. Light is a transverse wave – the medium must support shear stress (like a solid or a taut string, not like a simple fluid). Our space-medium acts in some ways more like an elastic solid (supporting transverse oscillations) than like air. In fact, one could think of it as an incredibly rigid “solid” that fills space. In classical wave theory, a medium that supports only transverse waves and no longitudinal mode is a bit unusual – it’s akin to an incompressible solid. By design, we chose the medium to behave this way to match electromagnetic observations.
• Frame of propagation: In ordinary media, wave speed is measured relative to the medium. For example, sound travels at ~340 m/s relative to the air. If you run fast, the sound coming toward you arrives a bit sooner (relative speed increases). With light, famously, no matter how fast you move, you measure the same speed c. How can that be if light is a wave in a medium? This was the great puzzle that led to Einstein’s theory of special relativity. The oceanic model must accommodate that experimental fact. The resolution (as envisioned by Lorentz and others) is that the medium is no ordinary material – it must somehow be Lorentz-invariant, meaning all inertial observers see the same laws. In practice, this means that moving through the medium does not produce the usual observable effects (no “wind” or Doppler shift of c). The mathematics of the wave equation is such that if it’s formulated in a Lorentz-covariant way (treating time and space coordinates appropriately), it’s consistent with relativity. In simpler terms, the structure of Eq. (2) with c constant is already hinting at Lorentz symmetry. The model can be made fully consistent by understanding that lengths contract and time dilates for moving observers (so everyone sees the wave moving at c). In a classical analogy, one could say the medium “goes along” with every observer due to how space and time transform – a concept very counter-intuitive in classical terms, but that’s essentially what the Lorentz transformation accomplishes. Historically, attempts to view the ether as undetectable (Lorentz’s ether theory) posited that objects deform in just the right way to mask any motion relative to the ether. Special relativity then reinterpreted that as there being no need for an ether at all. The oceanic model is effectively a reinterpretation that says: we can keep the idea of a medium if we also accept all the relativistic rules that make its detection via first-order effects impossible. In summary, while we liken our model to a classical wave medium, it is a very special kind of medium that doesn’t betray a “preferred rest frame” in the usual sense – a necessity to match the symmetry of Maxwell’s equations and experiments like Michelson–Morley (which found no difference in light’s speed due to Earth’s motion ).
• Energy and oscillation: In a classical medium, a wave’s energy oscillates between kinetic (motion of the medium) and potential (strain in the medium). The same happens in electromagnetic waves: energy swaps between the magnetic field (analogous to kinetic energy of the medium’s motion) and the electric field (analogous to potential energy stored in stretched configuration of the medium). This is more than an analogy – it’s quantitatively reflected in the form of energy densities. In our model, when \Psi is at a peak displacement (large |\Psi| but zero time-derivative), the medium has lots of elastic energy (electric field energy in EM terms), and when \Psi rushes through equilibrium (time-derivative large, displacement zero), the energy is kinetic (magnetic field energy in EM). This correspondence explains why E and B fields in a light wave are quarter-cycle out of phase and energy sloshes between them just like mass-on-spring or fluid oscillations. Faraday’s intuition of field lines under tension is directly realized here: field lines behave like stretched strings , with energy in the tension (electric part) and in motion (magnetic part).
In short, the oceanic model makes the wave nature of light completely explicit by providing the medium for the wave. What’s different is the extraordinary requirements for that medium to be consistent with relativity and the absence of any observed dispersion or preferred frame. It’s a mechanical wave model, but for a medium unlike any other – one that is ubiquitous, incredibly stiff, and yet inherently compatible with Einstein’s postulate that c is the same for all observers.
Maxwellian Electromagnetism – A New Perspective
Maxwell’s standard electromagnetic theory (as taught today) does not refer to any mechanical medium. Electric and magnetic fields are treated as fundamental entities – they interact with charges and with each other, they carry energy and momentum, and they satisfy Maxwell’s equations. The oceanic model does not change any of the successful predictions of Maxwell’s equations in vacuum; rather, it provides a potential mechanical underpinning for those equations. Here are key differences and points of contact:
• Unification of E and B: In standard EM, one often introduces the potentials \Phi and \mathbf{A} such that \mathbf{E} = -\nabla \Phi – \partial \mathbf{A}/\partial t and \mathbf{B} = \nabla \times \mathbf{A}. These potentials are a mathematical convenience (and become more in quantum theory), but they are not considered physical in themselves (one can add a gauge and change them without changing E,B). In the oceanic model, \Psi plays a role akin to \mathbf{A} (with \Phi perhaps encoded in \nabla\cdot\Psi if we allowed it). However, we treat \Psi as physical – a real state of the medium. Thus, what was a mere abstraction in Maxwellian theory becomes tangible. The electric and magnetic fields now have a common origin: they are just spatial or temporal derivatives of one field \Psi. This is a conceptual unification (one could say this model is a “hidden-variable” theory for the fields – the hidden variable being the medium’s displacement).
• Fields as stress and motion: Maxwell’s theory already contains the notion of field energy and stress. For example, the Maxwell stress tensor describes tension along magnetic field lines and pressure perpendicular to them . In our model, these are not just mathematical constructs – they literally correspond to physical stress in the medium (tension along the field lines because the medium is pulled taut by the vortex, pressure sideways because of the medium’s reaction to being stretched). So the oceanic model gives a clear physical interpretation to the field stress that Maxwell described. In Maxwell’s words, we are “explaining the electromagnetic force by means of a state of stress in a medium,” explicitly following Faraday’s conception . The difference is Maxwell used that as a way to rationalize the field concept, whereas here it is the physics: the stress is in the medium and causes forces. Similarly, Poynting’s vector \mathbf{E}\times \mathbf{B}/\mu_0 (which represents energy flow in EM) would correspond to actual energy flux via medium elements moving and dragging field energy along.
• Why no one talks about the medium now: Historically, Maxwell himself, after formulating the mathematical laws, grew agnostic about the exact mechanical model of the ether – he saw that the equations worked even without specifying the machinery. By the early 20th century, the Michelson–Morley experiment’s null result and the success of Einstein’s relativity (which assumes no ether) made physicists abandon the ether concept. The standard Maxwellian view, therefore, is content with fields existing as fundamental – they don’t need a mechanical explanation. The oceanic model challenges this by saying “maybe we just haven’t been looking at it the right way; the medium could be there, hidden in plain sight as the electromagnetic field itself.” It reframes standard EM by asserting that what we call “electric and magnetic fields” are manifestations of deeper oscillations of space itself. This is a bit reminiscent of how modern physics treats spacetime in general relativity – as something that can bend, stretch, and wave (gravitational waves). Here we’re saying spacetime (or at least space) can also have electromagnetic oscillations. We essentially return to Maxwell’s early idea that electromagnetic fields are a state of a medium, but we do so in a way that is consistent with all known laws (particularly relativity, which was a stumbling block for the 19th-century ether).
• New predictions or differences: In form, the oceanic model reproduces Maxwell’s equations, so one might ask: is there any observable difference at all? At the level of classical EM in vacuum, no – by construction it matches Maxwell’s theory for all experiments thus far. The differences are more philosophical unless we extend the theory. One potential difference is the existence of longitudinal modes (if \nabla \cdot \Psi were allowed not zero). Standard Maxwell theory has none in vacuum – if our medium had any hidden longitudinal vibrations, those could be a new physical phenomenon (sometimes dubbed “scalar waves” by various researchers). However, if the medium is exactly incompressible, then those modes are truly absent or perhaps exist at frequencies/energies we haven’t observed. Another difference is how this model might integrate with quantum physics – for instance, photons would be literally quanta of vibration of this medium (similar to how phonons are quanta of lattice vibrations in a solid). This could conceptually unify particle-wave duality in a mechanistic way (though developing that is beyond our scope here).
In summary, Maxwellian electromagnetism is “contained” within the oceanic model as a special case where we don’t ask what the fields are made of. The oceanic model provides a possible answer to that question: fields are made of a vibrating space-medium. This doesn’t change the successful computations of Maxwell’s theory, but it changes the storytelling: it provides an underpinning that was left out in the usual narrative. That underpinning has implications for how we think about unanswered questions (like how EM fields might unify with other fields, or what space is).
Why the Medium was Overlooked: A Historical Detour
If the oceanic model is so natural (waves need a medium, etc.), why was this idea overlooked or abandoned in mainstream physics? The story is a fascinating blend of experimental results and shifts in theoretical preference:
In the 1800s, the luminiferous aether was almost universally assumed. It was a logical necessity at the time: how else could light travel through empty space? Physicists imagined aether as an invisible medium filling space, extremely rigid (to have such a high wave speed) yet extremely tenuous (to not slow down planets or objects moving through it) . Many clever mechanical models were proposed – wheels, gears, vortices – to explain how this aether might produce electric and magnetic phenomena. Faraday, as mentioned, imagined lines of force that could be plucked like strings. Lord Kelvin and others tried to model vortex tubes in aether to explain atoms. Maxwell’s 1861 model used tiny vortices and idle wheels to derive certain electromagnetic laws . However, these models, while enlightening, were not uniquely determined – one could tweak them in many ways. The real nail in the coffin for a physically detectable aether came from experiment.
The most famous is the Michelson–Morley experiment (1887), which tried to detect Earth’s motion through the presumed aether “wind” by measuring the difference in light’s speed in different directions. The result was null – no detectable difference . This strongly suggested that either the aether is moving along with Earth (which raised its own issues), or that the premise of a stationary aether was wrong. At the same time, attempts to explain electromagnetism purely from within (like Oliver Heaviside’s reformulation of Maxwell’s equations and the emergence of the concept of fields as real entities) were gaining traction. Finally, Einstein’s special relativity (1905) eliminated the need for an aether by postulating that the laws of physics (including light’s speed) are the same in all inertial frames – essentially elevating what was a weird experimental fact to a fundamental principle. In Einstein’s framework, an ether at rest made no sense because no experiment could reveal it; it was an unnecessary entity. Einstein later in 1920 said one could talk about aether as long as it had no state of motion to be detected – but by then the word “ether” had become almost taboo, associated with discarded theory.
Thus, historically, the idea of a medium for light was overlooked not because it was illogical, but because it seemed unnecessary and undetectable. Physics shifted to focusing on the equations and symmetries (relativity, field theory) rather than mechanical underpinnings. Moreover, the rise of quantum mechanics made the notion of a concrete medium even murkier – fields became quantized, photons emerged as field quanta, and no classical substance was found.
The oceanic electromagnetic model reframes the discussion by saying: what if the field is the medium? That is, instead of two separate ideas (aether vs fields), we say the electromagnetic field itself is a manifestation of a medium. This medium doesn’t have a single universal rest frame in the observable sense – it is built to respect relativity (so it’s a very exotic kind of medium by everyday standards, perhaps better thought of as the “fabric of spacetime” that can oscillate). By being consistent with known physics, the model isn’t in contradiction with Michelson–Morley or other tests – those experiments ruled out a simple, naive aether (one you could measure motion against), but they do not rule out the existence of a pervasive field that has no accessible rest frame. In fact, modern physics has reintroduced the idea that vacuum is not empty: vacuum has energy, virtual particles pop in and out, and quantum fields fill space. These are not typically called “aether,” but philosophically, they serve a similar role – they are the substrate of reality. Our model is a classical take on this: treating space as a real medium with a classical field \Psi. It was historically set aside because of the triumph of Maxwell’s abstract field concept and relativity’s avoidance of aether, but we now recognize that thinking in terms of a medium can still be useful. It provides a visceral image (we can picture waves, stresses, and flows) and may guide intuition or new theories.
In reframing standard electromagnetism, the oceanic model doesn’t dispute any experiment; it repackages the theory in a way that might connect to other areas (for example, one could ask: is this medium related to the gravitational “fabric” of spacetime? Could a unified theory treat gravity and electromagnetism as different modes of a common medium? Such ideas hark back to the 19th century ether or to early 20th century unified field attempts). The model also reframes the question of what a photon is: instead of an irreducible quantum, a photon could be seen as an excitation (a quantum of vibration) of the underlying space-medium – much like a sound quantum (phonon) in a solid. This is actually quite aligned with quantum field theory, which says particles are excitations of fields. The difference is largely in language and interpretation: we’re using classical terms like tension and motion where QFT would use fields and quanta. But it’s intriguing that after a century of “no ether,” physics fields are back in a role that isn’t so different from a medium, albeit a quantum one . The oceanic model can be viewed as a bridge between classical intuitions and modern field theory concepts.
Experimental Outlook: How Could We Tell if Space is a Medium?
The ultimate test of a physical model is experiment. Since the oceanic model is constructed to give the same predictions as classical electromagnetism for usual situations, it’s challenging to find an experiment that distinguishes it. Nevertheless, a number of avenues exist to probe the idea that space has mechanical properties:
• Tests of Isotropy and Invariance: Experiments like Michelson–Morley have been done with incredible precision (modern resonator experiments confirm no light-speed anisotropy at the 10^{-17} level ). If the space-medium had a preferred rest frame and we were moving through it, we’d expect a tiny anisotropy in c or other effects. None have been seen, implying that if a medium exists, it either moves along with Earth (unlikely on a cosmic scale) or, more plausibly, that the medium’s laws are such that all frames are equivalent (as special relativity demands). Future experiments will keep improving precision, testing Lorentz invariance in ever more sensitive ways. So far, the results are fully consistent with the notion that any medium is Lorentz-covariant (effectively undetectable by uniform motion). If someday an anisotropy in the speed of light or a violation of Lorentz symmetry is detected, it would revitalize the idea of a detectable medium rest frame. However, current evidence strongly constrains any classical “wind” of aether.
• Longitudinal Waves (Scalar Mode): A striking prediction that could come from a medium model (though not inevitable) is the existence of another type of wave in the medium. If the medium were compressible to any degree, there could be a longitudinal wave (akin to a sound wave in the ether). This would be a very different beast from light: possibly carrying energy without carrying electric/magnetic fields in the usual sense, or coupling to matter very weakly. So far, no evidence of such a mode exists – if it did, it might show up as a new field or particle (some theories might call it an “ether wind” effect or a scalar field). We intentionally set \nabla\cdot\Psi=0 to match known EM behavior. But one could devise experiments to look for any trace of a longitudinal EM oscillation – for instance, in high-energy interactions or near electric charge oscillations, is there any emission of a scalar wave? If the answer is absolutely not, that supports the medium being strictly incompressible. If there were an observation (perhaps tiny deviations in inverse-square law at very short distances or unusual polarization effects), it could hint at new physics consistent with a compressible medium. This is speculative; mainstream experiments haven’t found anything like that yet.
• Vacuum Nonlinearity and Stress Tests: In our model, the vacuum medium could in principle have a nonlinear response if pushed hard enough (just as a real material eventually behaves nonlinearly if strained too much). Standard electromagnetism in vacuum is linear (waves don’t normally interact with each other in linear theory). However, we know from quantum electrodynamics that vacuum does exhibit subtle nonlinear effects at extremely high field intensities (due to virtual particle pairs, etc.). For example, very strong magnetic fields can make the vacuum behave like a birefringent material (polarized light travels at slightly different speeds – an effect being pursued experimentally with intense lasers and magnetic fields). One could interpret those phenomena as the “medium” showing its composition (the sea of virtual charges) – in other words, vacuum behaving like a material with a certain stiffness that can be polarized. If we push the analogy, experiments that measure vacuum birefringence or photon–photon scattering might be seen as testing the “elastic limits” of the vacuum. So far, these effects are extremely small and in line with quantum field predictions, but the oceanic model could encompass them qualitatively by saying the medium isn’t perfectly linear if you deform it violently (much like how a real ocean has waves that can break or form foam when driven hard). Future high-intensity laser experiments (such as those planned to reach unprecedented electric field strengths) could reveal new nonlinear responses of vacuum. If any surprise is found (something not predicted by QED), it might point to new physics in the vacuum – perhaps a substructure or medium-like property we didn’t account for.
• Analogical Experiments: Another way to “verify” the model is not by catching the actual medium in the act, but by reproducing electromagnetic phenomena in a laboratory analog system. For instance, hydrodynamic analogs have been studied: fluid vortices have been shown to mimic certain electromagnetic field behaviors . Recent experiments created little vortex rings in fluids and observed quantization of circulation analogous to magnetic flux quantization . Likewise, one could set up an array of coupled oscillators or use metamaterials to simulate Maxwell’s equations from underlying mechanics. If such systems exhibit all expected properties of light (including the “photon-like” discrete exchange of energy ), it bolsters the idea that a medium-based description is viable. While this doesn’t prove the real vacuum works that way, it provides a proof-of-concept. Notably, recent fluid-based models have even reproduced aspects of quantum behavior (e.g. analogs of Bell-test correlations in fluid waves ), suggesting that a deeper mechanical underpinning for electromagnetic phenomena is not outlandish. The oceanic model could be further validated by developing a small-scale physical analog that behaves exactly as the theory predicts (for example, a 3D network of springs whose wave modes correspond to E and B fields). If nothing else, this would serve as a teaching or visualization tool for how such a medium can work.
• Astrophysical observations: If space has a medium, could large-scale or high-energy phenomena reveal it? One idea: if there is a preferred frame (the rest frame of the cosmic medium), perhaps the cosmic microwave background (CMB) rest frame is it. We know we are moving relative to the CMB (there’s a dipole anisotropy). One could look for tiny variations in the propagation of light (say from distant pulsars or cosmic sources) correlated with that motion or direction. So far, none have been observed beyond what relativity already accounts for. Another aspect: gravitational waves are literally spacetime distortions – they do propagate at speed c and show that the “fabric” of the cosmos can wave. If one were inclined, one could think of electromagnetic waves and gravitational waves as two different vibrational modes of space: one primarily involving the electromagnetic medium properties, the other involving spacetime curvature. It’s speculative, but perhaps in extreme environments (like near black holes or in the early universe) the two could couple or influence each other. If space is a unified medium, a strong gravitational wave might slightly modulate electromagnetic propagation (beyond standard GR predictions) or vice versa. This hasn’t been seen, but future multi-messenger astronomy (observing events in both gravitational and electromagnetic waves) could, in principle, look for small cross-effects.
In essence, verifying the oceanic model experimentally is difficult because it so tightly imitates regular electromagnetism. The cleanest signature would be something that standard EM forbids – like a new kind of wave or a tiny violation of Lorentz invariance – but the model was built to avoid those, except where one extends it. So the task is either to push experiments to extremes where the “medium” might reveal itself (through nonlinearity or new modes), or to create analog experiments to increase our confidence in the concept.
So far, every classical experiment (double-slit interference, polarization, radiation pressure, etc.) is perfectly explained by Maxwell’s equations without needing a medium. The oceanic model explains them too, just in a different language. Therefore, it will likely take new technology or new regimes of physics to expose whether there is more to vacuum. Perhaps the answer will come from the quantum side – e.g. if we finally reconcile quantum physics and gravity, we might find that what we call “empty space” is indeed a kind of condensate or medium with many excitations (EM, gravitational, etc. all being modes of one entity). In that scenario, the oceanic electromagnetic model will look prescient: it would be an early classical foreshadowing of a deeper unity. But at present, it remains a theoretically intriguing alternative interpretation that must satisfy the same strict experimental bounds that any theory of space and light does.
Conclusion
We have presented a full exposition of the oceanic electromagnetic model – treating space as a tensioned medium and deriving electromagnetism from its wave dynamics. Starting from first principles (Newton’s laws and continuum mechanics), we arrived at a wave equation for the medium’s field \Psi. By defining electric and magnetic fields in terms of \Psi’s time and space derivatives, we naturally recovered Maxwell’s equations, explaining each term as a manifestation of the medium’s behavior. Along the way, we clarified how this model parallels Newtonian mechanics (force and inertia at every point), classical wave theory (with light as a transverse wave in a peculiar medium), and Maxwell’s field theory (which is reinterpreted rather than overthrown). We discussed why the idea of a physical space-medium fell out of favor historically – chiefly due to the failure of experiments to detect aether and the rise of relativity – and how the oceanic model revives it in a form that sidesteps those issues. Finally, we explored how one might test or find evidence for such a model, from ever-more-sensitive tests of light’s isotropy to searching for new wave modes or using analog systems to simulate the medium.
The tone of our treatment has been purposefully classical and visual: by envisioning fields as waves in an oceanic medium, we gain an intuitive picture without losing mathematical rigor. Every equation we derived was accompanied by an explanation of its physical meaning in the medium. The aim is clarity and insight – to feel that we understand electromagnetism as we would understand the vibrations of a drumhead or the waves on the sea. Whether or not nature literally employs this medium, the exercise deepens one’s appreciation of Maxwell’s equations and the unity of physical law. It reminds us that what we call “empty space” can be viewed as something rich and dynamic – perhaps the most fundamental medium of all, whose gentle ripples are the light that illuminates our world.